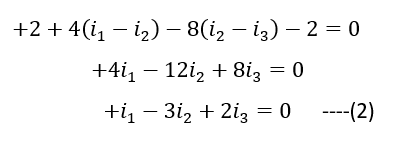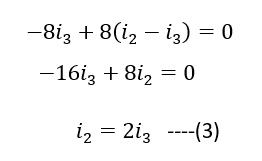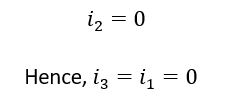Basic Electronics

---

Diodes are one of the very important components used in electronic circuits. These are one which help to safeguard your circuits. 

• For now, we will ignore what happens inside these diodes (e.g., p-n junction, holes, etc), which makes them work as they do. Let’s keep it for upcoming articles, but making its use in our project circuits is what we need, and that’s what we will be covering in this article.

1. Diodes have Polarity!

As we have already discussed about Resistors in our previous articles (Dealing with Resistors: Part 1 and Combining Resistors: Part 2 ), we know that Resistors don’t care in what way you are connecting them in circuits. 

• BUT for Diodes, it’s not the same! The way you connect the diodes in our circuit does matter. Hence, we have the terminologies of cathode and anode for a Diode.

2. Using Rectifier Diode

There are many types of diode but the most basic one is the rectifier diode. Diodes mainly behave like one-way valves. One-way valves only allow fluid to flow in one direction. If it flows in one, it can’t come or flow back in the opposite direction. 

• This is just a common analogy. You can say that the diode offers very little resistance to current in one direction, while it offers a very high resistance in the other direction, making the current difficult to flow in the other direction.

Understanding the flowchart below will help :

The circuits below show the Forward Bias and Reverse Bias Configuration for a Diode:

For connecting the Diode in Forward Biased Configuration :

• Connect the anode of the diode to a higher voltage and the cathode to a lower voltage

And for Reversed Biased Configuration :

• Connect the anode of the diode to the lower voltage and the cathode to the higher voltage

Diodes have a ‘constant’ voltage drop

We know that the voltage drop across a Resistor depends on the current passing through it. 

• Unlike Resistors, Diodes have a fixed voltage drop that doesn’t change with the amount of current passing through them.
• Generally, it is around 0.5V but depends on diode to diode. Checking the datasheet before calculations always helps!

By applying Kirchhoff’s Law in the circuit loop above, we get the voltage drop across Resistor R1 to be 8.5V. From this information, we can calculate the current in the circuit ‘i’ :

3. Conversion and Process of Rectification

Diodes can also help to convert AC Voltage to DC Voltage. Recall that AC has both a positive component and a negative component. If a diode allows one part to go through (say positive), the negative part won’t be allowed. 

• A picture will help in better understanding : 

The Voltage source finally does have just a positive part left (unidirectional like DC), but still, it’s not constant. It does have some fluctuations. To smooth this out and obtain a near constant voltage :

• Connect a Capacitor in parallel to a Resistor across the voltage source

BUT how does this combination of Resistor and Capacitor help to smooth out the given voltage signal?

Answer :

The capacitor smoothens out the fluctuations by charging and discharging in response to the ‘changing input voltage’. 

• When the input voltage starts rising, the capacitor charges up to store energy and matches the input voltage very fast
• When the input voltage begins to fall, the voltage across the capacitor doesn’t decrease rapidly even if the input voltage falls at a faster rate. The capacitor discharges very slowly, releasing its stored energy.

Hence, this process helps to decrease the fluctuations and hence obtain a near DC-like voltage signal

---

FAQ Section

Refer to the Following Sections of the Articles for more :

• Learning about Capacitors (Sections 2 and 3)
• Low and High Pass Filter Circuits 

Introduction

Low Pass Filters and High Pass Filters are two of the most important circuits to understand because of their extensive applications in electronics. In this article, we will explore their working principles, examine how they are constructed, and understand the reasoning behind their names.

1. What is Capacitive Reactance?

There’s a very common difference between a resistor and a capacitor : 

• In the case of a resistor, the resistance value remains constant, i.e., it doesn’t change even when varying the current or the voltage.
• But unlike a resistor, the value of capacitance depends on the current and voltage in the circuit.

We have already learnt about Charging and Discharging of Capacitors in the article: Learning about Capacitors. According to that, if our circuit consists of only a Capacitor attached to a battery, then :

• Capacitor blocks the DC current except at the time of charging & discharging
• Capacitor allows AC easily, as it is nothing but a cycle of charging, discharging, and recharging

Refer to the timeline diagram below, which shows how resistance to electron flow is offered by the capacitor during charging. 

Text Version of the above flowchart (Expand This)

1.Battery attached to uncharged capacitor.

2. Easy flow of electrons initially due to high potential difference (p.d.) ➜ less resistance.

3. Capacitor keeps on charging ➜ this makes the potential difference between the capacitor and battery to reduce.

4. As the capacitor is about to get fully charged, the current reduces ➜ strong opposition to electron flow.

This resistance offered by a Capacitor is referred to as ‘Capacitive Reactance.’

We denote it as ‘X_c‘

Capacitive Reactance is formulated as:

$X_c = \frac{1}{2\times \pi\times f\times C}$

where f represents the frequency of the source

Note: Here, I have shown a special case below

Case: DC Source is attached across the capacitor

Result: We all know that the frequency of the DC Source is zero, as there is no switching in polarity. Therefore, f=0 and we get reactance as infinite. Hence, we can see that the circuit almost behaves as an open circuit in the case of a DC Source.

Substituting f=0 in X_c formula:

$X_c = \frac{1}{2\times \pi\times f\times C} = \infty$

And also in case of AC Source, it is quite evident from the formula that, if the frequency of the source is increased, it results in a decrease of capacitive reactance. Let’s take 2 cases to understand this: Both are AC Source – One with f = 50kHz and the second with f = 10Hz (Capacitance is 10uF)

Hence, verified!

---

2. Using Ohm’s Law

• It is possible to use Ohm’s Law in this case as well. Just consider the capacitive reactance as some kind of resistor and then apply Ohm’s Law to it.
• But note that: Just one frequency at a time while using Ohm’s Law

Let’s calculate the peak current achieved in the circuits in the 2 examples considered in the previous section-1. The circuit has all the parameters the same, just the peak voltage of the AC Source is now given to be 5V.

3. Selecting Specific Frequencies

This frequency-dependent behaviour of capacitors makes them suitable for building some special types of circuits called Low Pass Filter and High Pass Filter Circuits.

• Capacitors block DC and allow AC. But with the help of these filter circuits, we can control which AC signals will specifically be allowed to pass. Hence, we call them filtering circuits

Just remember this analogy :

• Getting a voltage somewhere is equivalent to getting a signal over there.

3.1 Low Pass Filter

To understand this circuit, let’s take 2 cases: one at low frequency (f=0) and another at very high frequency. 

We can find the relation,

$V_{\text{in}} = V_{R} + V_{C}$

Case 1: Low Frequency (f = 0) of Source

This implies that the source behaves like a DC. And we know that, in steady state, V_c = V_out = V_in, i.e., the whole source voltage comes across the capacitor. 

Case 2: Very High Frequency of Source

At high frequency, the capacitive reactance is low → This makes the capacitor behave as a short circuit → This implies that there is no voltage drop across the capacitor → Therefore, V_c = V_out = 0

As discussed earlier, 

If we get a voltage at Vout, → It implies that we have the signal of that frequency over there. So, in the case of the above circuit, we are getting a voltage at Vout in the case of low frequency 

• Hence, as the above circuit allows low-frequency signals to pass (from input to output), the circuit is known as a Low Pass filter

3.2 High Pass Filter

To understand this circuit, Again lets take the same 2 cases: one at low frequency (f=0) and another at very high frequency. 

$V_{\text{in}} = V_{R} + V_{C}$

Case 1: Low Frequency (f = 0) of Source

This implies that the source behaves like a DC. And we know that, in steady state, V_c = V_in i.e. the whole source voltage comes across the capacitor. But V_out = 0 in this case, as V_out is now the voltage across the resistor (Therefore, V_out = V_R = 0)

Case 2: Very High Frequency of Source

At high frequency, the capacitive reactance is low → This makes the capacitor behave as a short circuit → This implies that there is no voltage drop across the capacitor → Therefore, V_c = 0. But, because of this, the whole source voltage shifts to the resistor. 

This makes V_R= V_out = V_in

If we get a voltage at V_out, → It implies that we have the signal of that frequency at the output. So, in the case of the above circuit, we are getting a voltage at V_out in the case of high frequency 

• Hence, as the above circuit allows high-frequency signals to pass (from input to output), the circuit is known as a High Pass Filter

---

Conclusion:

We have discussed the basics of the High and Low Pass Filter Circuits. The most fundamental difference between the two is the position of the output voltage. 

• In the case of low pass filters, V_out is set across the capacitor
• While in the case of High Pass Filters, V_out is set across the resistor

Keep Learning!

---

Combining what we have learnt in previous articles opens up a whole new set of ideas to explore. The combination of a resistor and Capacitors results in an RC Circuit. One of the very important types of electronic circuits to be studied is due to their wide range of applications.

Related Articles:

• Part-1: Dealing with Resistors
• Part-2 : Combining Resistors
• Part-1: Learning about Capacitors
• Part-2: More about Capacitors

---

1. Basics of RC Circuit:

1.1 Charging without a Resistor

Let’s consider a circuit with a battery of emf ‘E’ and a capacitor (capacitance ‘C’) connected in series to it via a switch ‘S’. Note that the capacitor is uncharged initially.

We know, charging will start as soon as the Switch ‘S’ is closed, and it is also seen that the capacitor gets charged very quickly. This is shown in Fig.2, where we plot the charge v/s time graph to keep a track of the charge appearing on the capacitor plates w.r.t time.

• When we say that a capacitor is fully charged, it means that the capacitor plates have the maximum charge they can hold. In this case, it will be ‘CE’. Also, this state where the charge doesn’t change anymore is called ‘Steady State.‘
• As the charge keeps on developing on the capacitor, the current in the circuit keeps on decreasing till it becomes zero at steady state. This whole situation, where every parameter(charge, current) is going through a change, is called ‘Transient state.‘

What happens when Resistance is added?

1.2 Charging with a Resistor

Now, we add a resistor with resistance R in series with the capacitor. The capacitor is uncharged initially. We have the most basic RC Circuit possible for analysis.

• We can sum up the role of a resistor here in simple words. It is mainly used to increase the charging time of the capacitor. This makes the transient state last a little longer. How long ?, can be decided and pre-calculated on the basis of R and C values chosen to build the resultant RC circuit.

In case of Charging, you can imagine a resistor as a cunning friend who doesn’t want you(the capacitor) to grow in his/her life. This friend somehow tries to delay the work that you would have achieved very easily earlier.

1.3 Discharging without Resistor:

Consider we have a capacitor, fully charged with the help of a battery of emf ‘E’, and we need to discharge it. 

• This can be done by simply disconnecting the battery and then allowing the two plates of the capacitor to be connected.

• Similar to the charging process, the discharging of a capacitor also happens instantly in the absence of a resistor. This can be seen in the plot in Fig.7

1.4 Discharging with a Resistor:

• In case of discharging, the resistor increases the discharging time. We can say that the resistor here acts as a good friend who doesn’t allow you(the capacitor) to fall(discharge) immediately.

Discharging still happens, but at a slower rate. This can be observed from the plot between q (charge on capacitor plate) v/s time ‘t’ as shown below.

So we can clearly see from Fig.8 that it takes time to reach 0 charge (for practical purposes). But how much time it takes is decided by the R and C values

---

2. Time Constant and its importance:

We represent ‘Time Constant’ by the Greek letter ‘Tau’ $(\tau)$

• Time Constant is mainly formulated as the product of the Resistance and the Capacitance. It’s an important representation mainly used in RC(resistance-capacitance) and RL (resistance-inductance) circuits.

$\tau = R \times C$

Now that we know how it is formulated, replace R X C with the time constant. 

Let’s start with the charging case :

$q = q_{0}\left(1 – e^{-t/(RC)}\right)$

$q = q_{0}\left(1 – e^{-t/\tau}\right)$

Inserting t = $\tau$

$q = q_{0}\left(1 – e^{-1}\right)$

$q= q_{0}\left(1 – \frac{1}{e}\right)$

$q = 0.63\, q_{0}$

On plotting the same, we get a graph shown below:

• From the above analysis, we can define time constant (For charging) as the time required to charge the capacitor to 63% of the total charge it can achieve, i.e., 63 % of the steady state charge

Let’s discuss the Discharging case :

$q = q_{0}\left(e^{-t/(RC)}\right)$

$q = q_{0}\left( e^{-t/\tau}\right)$

Inserting t = $\tau$

$q = q_{0}\left(e^{-1}\right)$

$q = \frac{q_{0}}{e}$

$q = 0.37\, q_{0}$

• Again, from the above analysis, we can define time constant (For discharging) as the time required to discharge the capacitor to 37% of the total charge it had initially, i.e., 37 % of the steady state charge

We can keep on inserting such time values and keep a track of the charge on the capacitor.

Important: Note that q is the charge on the capacitor plates at time instant ‘t.’

Charging case:

• It is seen that approximately after a minimum (t = 5 * time constant), the capacitor is 99% charged. We consider that as approx fully charged in reality while doing some projects and all!

Inserting $t= 5\tau$

$q = q_{0}\left(1 – e^{-5\tau/\tau}\right)$

$q = q_{0}\left(1 – e^{-5}\right)$

$q = 0.99q_{0}$

Discharging case:

• It can be seen again from the calculations below that, –> It takes about (t = 5 * time constant) to discharge the capacitor to an extent where only 1% of the initial charge remains on the plates.
• We consider this as approx. fully discharged case for project purposes  

Inserting $t= 5\tau$

$q = q_{0}\left(e^{-5\tau/\tau}\right)$

$q = q_{0}\left( e^{-5}\right)$

$q=0.01q_{0}$

---

Conclusion:

So, based on our previous articles’ knowledge (Resistors and Capacitors), we have learnt about the basics of the RC Circuit. There will be another article to go into further depth in the case of RC Circuits.

• Have a look at the derivations, as those will provide a proper insight and reasoning of why exactly things happen in that way. It’s always good to have a look at the mathematical analysis of the physics concept you study!

Keep Learning!

---

In Part-1: Learning about Capacitors, we already got an idea about the functioning of the capacitors. But now, with that understanding, how to make use of them in electric circuits?

This is what we focus on in this article. Getting inclined towards the numerical aspect of the capacitors is our goal for this article.

1. Clearing the basics

As discussed in part-1, the more the charge separation happens (+Q on one plate and -Q on the other), the more will be the potential difference across the plates of the capacitor(V). So basically we can say, 

$Q \propto V$

Now we introduce the ‘constant’ of proportionality –> Capacitance (C). The relation becomes :

$C = \frac{Q}{V}$

Note that :

• Increasing the charge doesn’t increase the capacitance of the capacitor as it may appear in the above equation. For simplicity, remember it as –> Once a capacitor is made, its capacitance value is stamped on it !!
• Instead, capacitance is decided by the physical dimensions and the dielectric used. (For understanding, once the vessel is manufactured, it has some dimensions to it, and based on those dimensions, you can decide the capacity of the vessel.)

---

2. Parallel Plate Capacitors

There are many configurations possible to make a capacitor, but the simplest one to analyze is the Parallel plate Capacitor. This setup basically consists of :

• 2 metal plates of area ‘A’ kept at a distance ‘d’ apart from each other
•  Dielectric medium (of dielectric constant ‘k’) inserted between the plates
• Important Condition : (A>>d)

The capacitance of the parallel plate capacitor is given by :

We can clearly verify from the above expression that the capacitance just depends upon the geometrical factors and the dielectric constant.

---

3. What is a dielectric, and what is its use?

“In simple words, dielectrics are a type of insulating materials which allow Electric field but doesn’t allow an electric current to pass through them.”

They are mainly used to serve 3 purposes: 

Purpose of using Dielectric (Expand This)

There are 3 purposes to use a dielectric –

1. A dielectric acts as an insulating material that maintains the gap between the plates
2. It increases the maximum voltage that can be applied across the capacitor plates without getting breakdown
3. It increases the capacitance of a capacitor

3.1 Maintaining Gap

It is necessary to maintain the gap (even though small) between the metal plates. Because the capacitor would lose all of its storing capacity if the metal plates come in contact with each other, since in that case, it would just behave as a simple conductor.

3.2 Increasing the maximum voltage without breakdown

Dielectric Breakdown: 

• Each dielectric material has its own breakdown voltage. 
• If the applied voltage becomes greater than the breakdown voltage of the dielectric material, the atoms start to get ionized, and we know that ions do conduct electricity. 
• Because of this, the whole capacitor starts to act as a conductor 

The better the dielectric material, the higher the dielectric breakdown voltage. Let’s consider 2 situations :

The dielectric breakdown voltage of the material (say D2) is more than that of air. This implies that more voltage across the capacitor plates is required in the case of D2 for the breakdown to happen. This proves our point that the insertion of a dielectric allows us to apply more voltage across the capacitor plates without causing any dielectric breakdown.

3.3 Increasing Capacitance

Suppose we have a capacitor with just air between the plates. Now we insert a dielectric material of dielectric constant ‘k’ between the plates completely. Have at the look at the flowchart below to just get a quick overview of what happens!

4. Series Combination in Capacitors

“Like the way we have current in case of resistors, in the same way, for capacitors, we have charge.”

• For Capacitors to be said in a series combination, the charge flowing through them should be the same.

Consider 3 capacitors C₁, C₂, and C₃ in series combination, and V₁, V₂, and V₃ are the potential differences across them, respectively.

Since we need to find the ‘equivalent’ capacitance :

$V_{\text{eq}} = V_{1} + V_{2} + V_{3}$

$\frac{q}{C_{\text{eq}}} = \frac{q}{C_{1}} + \frac{q}{C_{2}} + \frac{q}{C_{3}}$

But the charge flowing through all is still the same. Hence, we get:

$\frac{1}{C_{\text{eq}}} = \frac{1}{C_{1}} + \frac{1}{C_{2}} + \frac{1}{C_{3}}$

So, we can observe that, by keeping capacitors in series, we get the value of equivalent or resultant capacitance, which is even less than the one that has the least capacitance among the three. Suppose,  C₂ < C₁ < C₃, then C_eq < C₂ 

5. Parallel Combination in Capacitors

Again:  “Like the way we have current in case of resistors, in the same way, for capacitors, we have charge.”

• For the Capacitors to be in Parallel, the potential difference across all should be the same.

Consider 3 Capacitors C1, C2, and C3 in parallel combination, and the charges passing through them are q1, q2, and q3, respectively.

We know the relation from KCL : 

$q = q_{1} + q_{2} + q_{3}$

$C_{\text{eq}}(V) = C_{1}(V) + C_{2}(V) + C_{3}(V)$

But the potential difference across all is still the same. So, we get:

$C_{\text{eq}} = C_{1} + C_{2} + C_{3}$

The equivalent capacitance incase of a parallel combination will be greater than the greatest among the three (here)

6. Methods to simplify the circuits

Now, there are again some types of network circuits in which we are expected to find the equivalent Capacitance. 

There are several methods to simplify and solve such type of circuits, like :

• Mirror Symmetry
• Folding symmetry
• Voltage method (Rearrangement)

We have already looked at the above methods with context to resistors in Part-2: Combining Resistors.

Though the article is for Resistors, the approach of simplifying the circuit/network still remains the same!

How to approach the problem?

1. Simplify the given complex circuit using the methods discussed already in the linked article, i.e., Mirror Symmetry, Folding Symmetry, etc.
2. You will get the simplified circuit in the form of series and parallel connections
3. Use the discussed concept to solve the series and parallel combination of capacitors

---

7. Special equivalent capacitance problem :

Example: Find the equivalent capacitance across points A and B

Step-1 :

Distribute the voltages across all plates. In this example, we consider the voltage/potential at A to be ‘a’ and at B to be ‘b’. Still, we are not able to cover all the plates. So we introduce another unknown potential ‘x.’

Remember that: Potential always remains constant on a conductor

Step-2 :

Assign the numbers to each face of the plates 

Step-3 :

Keep points ‘a’ and ‘b’ at the ends, and all the unknowns which we introduced should come in between.

Step-4 :

To make a capacitor, we need 2 plates and separate them by a distance

• Faces 2 and 3 make a capacitor
• Faces 4 and 5 make a capacitor
• Faces 6 and 7 make a capacitor
• Faces 8 and 9 make a capacitor

So, now, we just look at the numbers assigned to their faces and make a simplified circuit.

Step-5 :

Solve by normal Series- Parallel concepts

The equivalent capacitance of the simplified circuit is 5C/3,  where C is :

$C = \frac{A \,\varepsilon_{0}}{d}$

---

Conclusion:

• So, with this, we are done studying about combining the given capacitances in various patterns to get the required capacitance in our circuit. Also, in previous articles, we have learnt about Resistors – Part 1: Dealing with Resistors and Part 2: Combining Resistors
• Just combining these 2 components – Resistors and Capacitors opens up a whole new set of things that can be developed. We will be looking into these in our upcoming articles.

Till then, Keep Learning!

Author: Saurabh Salvi

• Let’s consider a ceiling fan at rest (switch is off). Now, I turn on the fan. Here, the thing is that an initial burst of energy is required to make the fan just start rotating from rest. Once it has gained momentum, it consumes much less energy. To provide that initial burst of energy, capacitors come in handy.

• We can compare this situation with ourselves when we were at school. It’s time to get ready for school in the morning, and we are peacefully sleeping in bed. And out of nowhere, Mom enters the room and spanks us to wake us up! But once we wake up, we used to manage all the things smoothly. So, in this example, our mom acts as a capacitor to give us that initial boost/burst which is required to get us out of bed.

This was just one of the many uses of a capacitor. Also, combining a capacitor with other components opens up even more interesting ideas.

Capacitors as storage devices

• Capacitors are mainly known for their ability to store electrical energy in the form of charge, and they provide it at once when needed. But this electrical energy is obtained by the capacitor itself from another external voltage source

Basic Structure of Capacitor includes :

• Two metal plates separated by a distance
• A dielectric inserted between the plates

Note: For now, assume the dielectric to be some substance that doesn’t conduct electricity easily and is something used to enhance the storing capacity of a capacitor.

---

How is the charging and discharging of a Capacitor done? (Important)

Charging of Capacitor:

• Let us go step-by-step to understand what exactly happens when a capacitor gets charged. Also, simultaneously, we will take an example of 2 friends, A and B; the batteries actually refer to the minds/amount of knowledge of the individuals. Friend A is analogous to a battery, while Friend B is analogous to a capacitor.

Step-1 :

Step-2 :

Note :

• Negative terminal of the battery can be considered to have a cluster of free electrons (a lot of electrons), and because they are free, they tend to move across the circuit
• Wherever there is a separation of charges, a potential difference will start to build up

• Now, while moving, these electrons reach the capacitor plate and start accumulating (as there is no wire as such for electrons to keep moving) on the plate, causing an excess of electrons on the plate. This makes the plate become negatively charged (-).
• Simultaneously, we have electrons from the other plate getting attracted towards the positive terminal of the battery. This causes a deficiency of electrons on the capacitor plate. This makes it positively charged (+). In this process, the electrons move through the bulb as well, which makes the bulb glow (but only for a short time, as discussed below).
• As mentioned in ‘Note’ above, a potential difference (P.D.) will be created across the capacitor (but still V(battery) > P.D. across the capacitor)

Gradually, there is an increase in the amount of knowledge (P.D. across the capacitor) of B. B has gained this knowledge from A (battery).

Step-3 :

The Step-2 keeps on happening (battery keeps pushing electrons to one plate and keeps pulling electrons from another plate) until V_battery = P.D. across the capacitor. Because it implies that there is sufficient negative charge on the plate, which is capable of repelling the coming electrons (and also there is enough positive charge developed on the other plate to keep the electrons attracted to itself).

• We call this condition of a capacitor as ‘saturated condition.’
• This stops the electron flow in the circuit, and the bulb doesn’t glow anymore

Coming to our example/analogy,

The figure shown below is an example of 2 friends (Friend A and Friend B) for step-3

At this saturation condition (here), we call the capacitor to be fully charged !!

Quick Question!

Comment on the number of charges present on the whole capacitor at initial t = 0 situation and after charging.

Answer: The number of charges/electrons remains the same in both situations.

Remember that: Positive charge is nothing but a deficiency of electrons, while negative charge is just an excess of electrons.

In the example below, after charging, a charge of +2 appears on A because there is a deficiency of 2 electrons, but these electrons are added to B, causing an excess of 2 electrons. But as a whole capacitor, the total number of electrons remains the same.

---

Some Cases (Covers Discharging of Capacitors):

Case 1:  We disconnect the battery from the circuit and leave it open

We can see that the charge still remains on the capacitor even after disconnecting the battery as the circuit is opened and there is no current flow possible across the circuit

Case-2 : Discharging of Capacitors

What did we do?

• We replaced the battery with the wire -> This basically closes the circuit

What happens?

• Electrons start flowing from the negative plate (excess of electrons) to the positive plate.
• While moving through the circuit, the electrons pass through the bulb, which causes the bulb to light up.
• But this goes on only till the positive charge gets vanished (due to neutralization done by electrons), and simultaneously, the negative charge on the negative plate also reduces as electrons leave the plate
• When there’s no charge on the plates -> no potential difference -> no current -> the bulb goes off.

---

3. Capacitor says: “I oppose voltage change!”

• Capacitors are those that don’t adapt to changes very quickly. They take some time!
• As seen in the above section, a capacitor doesn’t charge up immediately on connecting it to a battery. It does take some time to build up the charge
• Similarly, on replacing the battery with a wire, i.e., discharging the capacitor, the potential difference across the capacitor doesn’t become 0 immediately. It took some time for that to happen

Overall, the inference that we can take is that Capacitors oppose voltage change. It takes time for the capacitor to reach the target voltage applied across it.

But for Resistor, the case is different. It adapts to the change very quickly, unlike capacitors.

---

4. How does Alternating Current (AC) pass through capacitor?

• In the case of DC, the current flows through the capacitor only for a short interval of time

Now, coming to AC, our main goal is to study how capacitors deal with an AC source exactly.

We will again go step-by-step to understand the procedure, and also have our 2 friends’ example alongside for better understanding.

• But note one important difference that in the case of a DC source, the knowledge of A was always full (constant), but now, since we are dealing with AC, for example, the knowledge of A will also vary!

An AC source can be represented as a sine curve (just to show one of many AC curves):

We divide this thing into 4 parts :

1. 0 to +peak
2. +peak to 0
3. 0 to -peak
4. -peak to 0

Step-1: starting at t=0, the AC voltage is going  from zero towards the peak, & Capacitor is uncharged

• The voltage of the AC Source is going on increasing. This causes electron flow in the circuit as charges start developing on the plates of the capacitor.
• At V= +peak, the capacitor might be fully charged or charged to some extent (let’s consider the second case(i.e., charged to some extent))

Coming to our 2 friends example. Again, reminding: Friend A represents the power source (AC Source here) while Friend B represents the capacitor. Initially, both have zero knowledge here (as the AC voltage is zero, and also the capacitor is uncharged initially).

Step-2 : AC voltage from +peak to 0

• Now, after reaching the peak, the source voltage is starting to decrease, BUT as discussed already, the capacitor opposes voltage change, so the P.D. across the capacitor is still at the same value as it ended in the step-1.
•  A time will come when the source voltage will become less than the P.D. across the capacitor.
• At that time, the positive plate of the capacitor will have more strength than the positive of the AC source. This will cause electrons to get attracted more towards the positive end of the capacitor. This will eventually cause the discharge of the capacitor.
• Due to discharging, the current flow reverses, but electron flow is still there through the bulb, which makes the bulb continue to glow.

Coming to the Friends’ example

Step-3 : AC voltage goes from 0 to -peak

• As soon as the AC voltage enters negative y, it implies that the polarities of the AC Source get reversed. This will cause the capacitor to immediately get discharged completely (THINK!)
• Once discharged completely, charges will start to get developed in an opposite manner (the plate that was positive earlier becomes negatively charged this time, while the plate that was negative earlier becomes positively charged now).
• Basically, the capacitor is again ‘Recharging’.
• And still, as there is a flow of electrons through the bulb -> it will keep glowing.

Friend B is about to get discharged, and as soon as V_source reaches some negative value, the capacitor gets completely discharged, after which, Recharging starts!

Step-4 : AC Voltage goes from -peak to 0

• The source is again returning to zero, which means that the strength of the source is reducing. And again at some instant, the source voltage and P.D. across the capacitor will become the same. After this instant, once the voltage further reduces to approach zero, the capacitor gets ‘more strength’ than the AC source.
• This will cause electrons to get more attracted to the positive plate of the capacitor. This will cause the discharging of the capacitor plates (as the electrons start neutralizing everything)

Observation and Inference:

• From the above steps, we can observe that the bulb never really stops glowing when AC voltage is applied. This shows that there was a continuous flow of electrons through the bulb. (To glow, the bulb just needs electrons to flow through it; it literally doesn’t care about the direction in which the electrons are flowing through it.)
• So, basically, the continuous cycle of Charging, Discharging, and recharging keeps the electron flow happening in the circuit.

---

For Best Experience, View on Desktop/Laptop !

In Part 1 : Dealing with Resistors, we learnt about the Resistor, basically how it works, what are it’s application, how to use in circuit, etc. But we come across the circuits which involve some combinations of resistors. Our aim in this article is to simplify these network and obtain Equivalent Resistance of the network.

Topics Covered :

• What is meant by finding equivalent resistance ?
• Resistor in Series
• Resistor in parallel
• Example on Series – Parallel
• Folding Symmetry & Example
• Mirror Symmetry & Example
• Voltage method (Rearrangement) & Example
• Assignment & Conclusion

1. What is meant by finding equivalent resistance ?

When it comes to circuit solving, we will encounter lot of complex combination of resistors present in the circuit. Finding ‘equivalent’ of such combination of resistors means that, we must be able to replace that whole thing with just a single resistor without changing any of the other parameters (current, potential difference across given points, etc. ) in the circuit.

Fig.1                                             (a)                                                                                                                         (b) 

Note that, in Fig.1 (a) and (b), except the number of resistors, there is no change in other parameters (I remain I, E remains E, delta V remains delta V)

Now, how to actually calculate this value of Req is what we need to study in this article !!

2. Resistors in Series

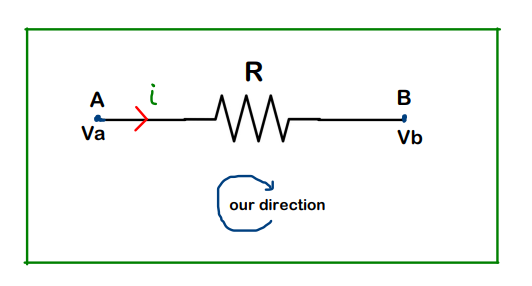
Resistors are said to be in Series when the current flowing through them is the same. Done !

Now, with reference to above figure,

Important Note :

From the above relation, we can infer that, we can use series combination if we need a resistance value greater than the individual resistances (i.e. Req > R1 & also Req > R2)

So, Resistors in Series just add up directly !

3. Resistors in Parallel

Resistors are said to be in parallel, when they have same potential difference across them. Done !

Important Note :

From the above relation, we can infer that we can use parallel combination if we need a resistance value even lower than the individual resistances. (i.e. Req < R1 & also Req < R2)

Breadboard Connections for parallel combination :

4. Example on Series – Parallel

Question -1

Find the equivalent resistance of the given setup across points A and C

Solution :

Step – 1 : Both the 4ohms resistors are connected across same points B and C. Hence, Both are in parallel combination. Req for just this combination will be 2 ohm

Step-2 : Now, 5ohm and 2 ohm are in series combination. Req of this will be 7ohm

Step-3 : Finally, we have 7 ohm resistor between A and C. This is our final Req between points A and C

Question – 2 :

Solution :

Step 1 : same current passes through AF and FE which makes both the 3 ohm resistors in series. Req for this will be 3+3 = 6 ohms

Step 2 : Two 6 ohm resistors are connected across same points A and E which makes them in parallel. Req for this will be 3ohm

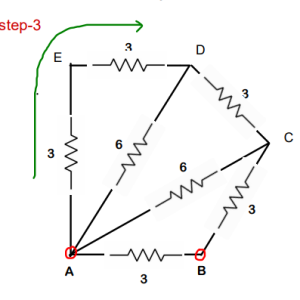
Step 3 : again both 3 ohm are in series. Req will be 6 ohm

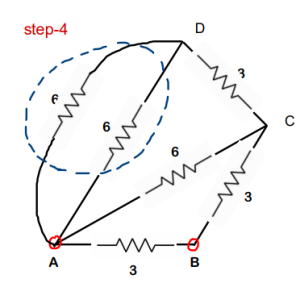
Step 4 : both 6 ohm are in parallel. Req will be 3 ohm

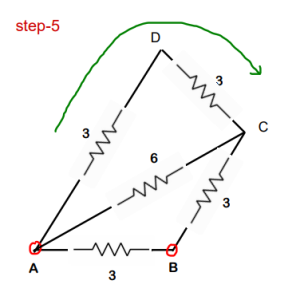
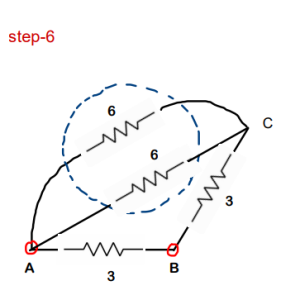
Step-5 : 3 ohm and 3 ohm are in series. Req of this will be 6 ohm

Step-6: two 6 ohm resistors are in parallel. Req of this will be 3 ohms. Keep on simplifying !!

Step-7 :  3 ohm and 3ohm  are in series

Step-8 : 6 ohm and 3ohm are in parallel. Req of this will be 2ohms.

Final Answer : So, the overall equivalent resistance across points A and B is 2ohm

5. Folding Symmetry

(Example will make everything very clear, but keep the below idea in your mind)

• Step 1 : Consider a line passing through the points across which equivalent resistance needs to be found. Let this line be called AB for now.
• Step 2 : See if any folding symmetry exists. Folding needs to be done about the line AB. (By folding symmetry, we mean that there should be an exact overlap once the folding is done).
• Step 3 :Once folding symmetry is confirmed, it implies that all the potentials are also identical at the overlapping points

Let’s take an example to understand this !!

Example :

Solution :

Step-1 : We need to find equivalent resistance across A and B. So we draw line AB first

Step-2 : So we fold one portion of the network about AB and see if it coincides with the portion on other side (Just like a folding of chapati about it’s diameter). And here it does !! – Folding symmetry exists !

Step-3 : Now, since Folding symmetry exists,  Vc=Vh (Potential at ‘c’ = Potential at ‘h’) ; Vd = Vg ; Ve = Vf.  This implies that the potential difference for the resistor between points ‘A’ and ‘c’ is equal to the potential difference for the resistor between points ‘A’ and ‘h’. This again tells us that, they are in parallel. So, we can just keep one of those resistors but it’s value will become ‘R/2’

(Read it again !)

(We follow similar process for all the remaining resistors & we get the circuit shown below)

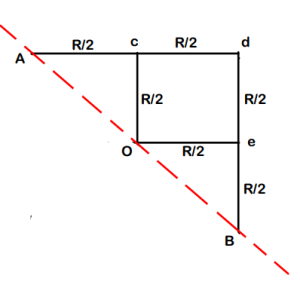
Step-4 : Just solve this like a normal Series- Parallel problem

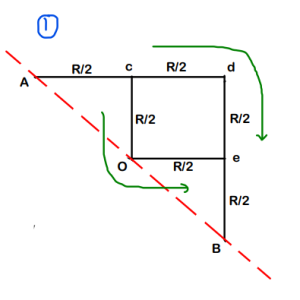
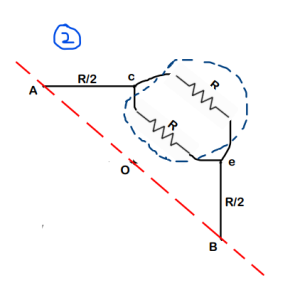
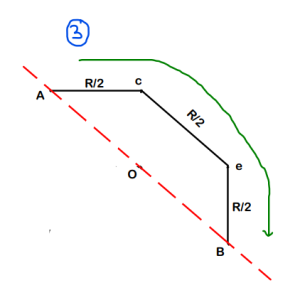
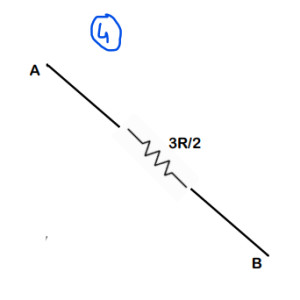
Final Answer : We get the overall equivalent resistance as 3R/2. So option (b) is correct.

6. Mirror Symmetry

• Just check for mirror symmetry about any line (imaginary is also OK) in the circuit
• If any mirror symmetry exists, then the currents in the mirrored branches should also be same. This point is responsible for simplification of the circuit.

Let’s take an example to understand this even better !

Example :

Find the equivalent resistance of the circuit shown in the figure about points a and b. Each resistor has a resistance ‘r’

Solution :

Step-1 :

• Draw the imaginary line about which you find mirror symmetry.
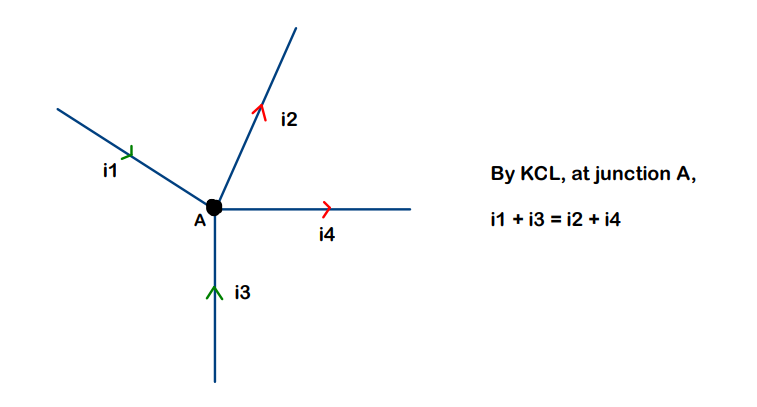
• Consider as if a current ‘i’ enters the whole network through A and gets distributed in branches such that ;                                                i = i1 + i2 + i3
• Because of mirror symmetry, the current in corresponding image branches should also be same and an overall current ‘i’ should come back from B 

Step-2 :

• ‘i1’ flows in AC and as discussed in step-1, ‘i1’ flows in CB as well
• But applying KCL(junction rule) at C, current ‘i1’ should have been distributed in branches cd and cB. but it doesn’t happen as the whole current ‘i1’ goes into branch cB
• This implies that resistor between points c and d is not actually attached at C even though it just appears to be attached. We can just remove it’s connection

Step-3 :

• Similar thing with i2 !!The current in Ad (i2) should have been divided at ‘d’
• But the whole i2 gets passed on to dB which implies that the resistor is actually not connected to ‘d’ as well (because if it was, then current would have been divided)

Now it is just simple Series-parallel Problem !!

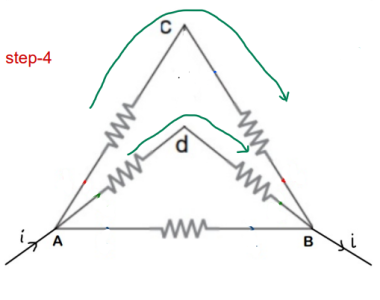
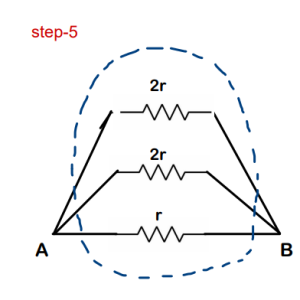
Final Answer : The overall equivalent resistance of the circuit across the points is ‘r/2’

7. Voltage method (Rearrangement) 

This method is to be used when we are not directly seeing any kind of symmetry. This method is basically rearrangement of the network in order to get a clearer view to proceed further

Remember :

• Potential remains constant along the plain wires.
• Resistors connected across same potentials are in parallel

(Example will make it more clear)

Procedure :

• Step-1 : Distribute the potentials across the whole circuit. Take care that potential should be defined across both the ends of each resistor. Introduce new variables to denote unknown potentials if needed.
• Step-2 : Number the ends of the resistors
• Step-3 : Write down the potentials separately , keeping the points across which the Req is to be found at the two ends
• Step-4 : Place the resistors between their respective potentials

Let’s take an example to understand this even better !!

Example : Find equivalent resistance of the given circuit about points ‘a’ and ‘b’

Solution :

Step-1 :

• As we already mentioned, potential along plain wires remains constant.
• We are unaware of the potential at the center, so we consider it as ‘x’

Step-2 :

• Number all the ends of the resistors. (Complete one resistor first and then proceed to next !)

Step-3 :

• Now, separately write down the potentials
• Remember that the points/potentials across which you are calculating equivalent resistance should be kept at the ends

Step-4 :

• Observe and connect the numbers to the respective potentials (a –> 4 ; x–> 3,5,2,7 ; b–>6,1,8 )
• On completing this, you will get a clear view of what the circuit actually was !!

Now, it is just simple Series-Parallel problem !

Final Answer : The equivalent resistance of the circuit between a and b is 4r/3

8. Dealing with Wheatstone Bridge

• The below wheatstone configuration is often seen while solving problems based on equivalent resistance.

(I am just adding this so that you don’t feel stuck at any problem just because you were not aware of this !!)

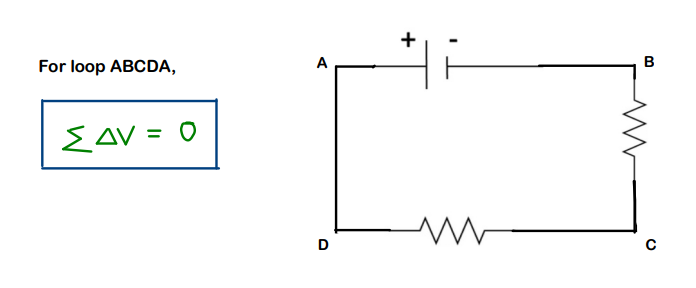
9. Kirchhoff method for Req

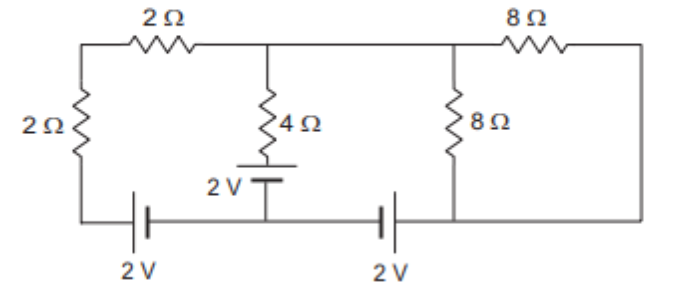
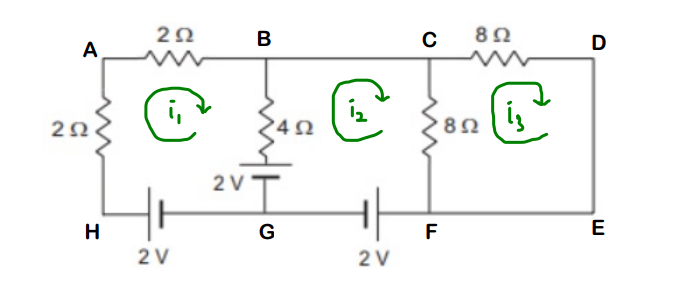
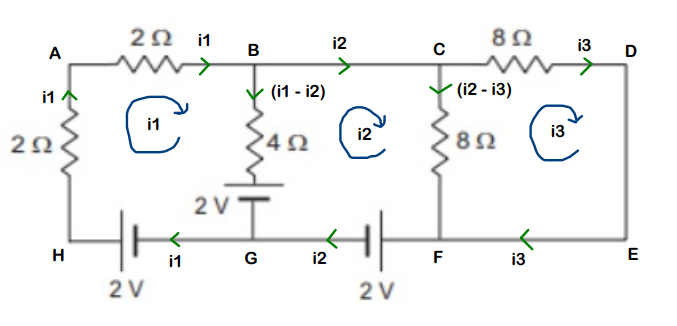
When nothing works at all, there is always Kirchhoff method to the rescue !!

• We have already discussed it in the article : Tackle circuits using Kirchhoff’s Laws

10. Assignment & Conclusion :

• So now on completion of both the parts : 1st – Dealing with Resistors and this 2nd- Combining Resistors, We have a good foundation set to understand electric circuits in a much better way.

• This second part was mainly to go into much more depth for understanding circuits based on resistors. later on, we will add capacitors, inductors as well to expand our applications !!

Based on this article, some problems have been shortlisted from popular books, so that you can have a practice kind of thing as well. Solution to this assignment can be asked through email.

For solutions or doubts,

email at : physicsandelectronics079@gmail.com

DOWNLOAD

Combining Resistors - Assignment

All the Best !!

Keep Learning !!

Consider 2 situations. For the first case, suppose you are running freely on an open ground; for the second case, consider yourself running at the Mumbai local station (that too during peak working hours). Immediately, you will notice that you can’t run that freely in the second case. What’s the reason? 

Resistance. The crowd at the railway station acts like an obstruction for you while you try to run. A similar obstruction is felt by those tiny electrons while moving from the conductor. We term the difficulty that electrons face in flowing due to the object’s opposition’Resistance.‘

---

1. What factors affect Resistance?

1.1 Material:

• Materials that are good conductors allow easy flow of electrons through them since the nucleus in the atoms doesn’t influence the valence electrons much, due to which they get easily detached from the atoms and contribute to the current. (Imagine atoms of conductors as not-so-strict parents).
• On the other hand, we have insulators that don’t allow electrons to flow freely. This is due to the very strong influence of the nucleus on the valence electrons, and because of this, the electrons are tightly bound to atoms. (Imagine atoms of insulators as very strict parents)

We refer to this property of material as ‘Resistivity‘.It is basically a characteristic of the material. So, conductors have lower resistivity as compared to insulators since they offer less resistance to electron flow for a given volume.

1.2 Cross-sectional Area:

• From our daily life experiences, we know that driving on a broad highway feels much freer than driving on a narrow road. Because of this, the first thing we try to do on the highway is to speed up our vehicle. On a similar basis, when the area of cross-section of a wire is greater, the resistance is lower, hence making electron flow easier.

1.3 Length and Area of Cross-Section:

• The longer the length of the wire/object, implies that more atoms/molecules will interact with the electrons, hence increasing the obstruction. So, Resistance is high in this case

Taking into account all the above 3 factors (Material, Cross-sectional Area, and length), we can compress it into a formula as: 

$R = \frac{\rho \times l}{A}$

• R is the resistance
• $\rho$ is the Resistivity – a property of the material
• A is the area of the cross-section
• l is the length

Question: Given below is the cross-section of a wire, and the direction of current is shown for each case. Write down the expression for resistance R for each of the cases (case-1,2,3)

Solution :

Important to Note : In the formula of R, rho is the resistivity, L is the length (along the current direction), and A is the area of cross-section (current passes through this section of area while passing)

CASE-1:

Final Answer for the case-1:

$R = \frac{\rho b}{l w}$

CASE-2:

Final Answer for Case-2:

$R = \frac{\rho l}{b w}$

CASE-3 :

Final Answer for Case-3:

$R = \frac{\rho b}{l w}$

1.4 Temperature:

Usually, in normal cases, as the temperature increases, the resistance is seen to increase. There is also a relationship between the resistance and the temperature.

$R = R_o (1 + \alpha \Delta \theta)$

• $R_o$ is the original/initial resistance
• $\alpha$ is the temperature coefficient of resistance
• $\Delta \theta$ is the temperature difference

2. Use of Resistors in Circuits:

Ok, so now coming to the main portion: what is the actual use of a resistor in any electronic circuit !? Answering this question, there are 2 main uses of a resistor :

• Limiting the current 
• Controlling the voltage

2.1 Limiting the current:

Resistors are commonly used to make sure that only the current required by the device goes into it, nothing more! Getting excess current than required can damage the devices very badly (i.e., it might even burn them off This happens mostly with sensitive elements like LEDs, ICs, transistors, etc.)

Let’s consider a problem.

Suppose that you need to make a red LED glow with the help of a 9V battery. So, shall we just directly connect the 9V battery to the LED? What happens if we do that?

Basically, if we directly connect the battery to the LED, there is a lot of current flowing through the LED, which causes it to ‘burn’. Excessive current to the sensitive components fries them up !! So, what’s the solution for this?

• Just add the appropriate resistor with the LED. This resistor will ensure that only a sufficient amount of current is passed from the LED

How to decide the resistance value?

For the problem, we have :

• A 9V battery
• Red LED (maximum safe current – 20mA and forward voltage drop of 2V)

Note:

Every component causes a voltage drop when current passes through it. For LED, we call it ‘forward voltage drop’. The word ‘forward’ comes due to the reason that the diode only allows current to flow in one direction, due to which the voltage drop will also happen in the forward direction only. 

Now, for the analysis part :

Our main aim is to find the value of ‘R’. We are considering 20mA current to be flowing in the circuit because it’s the maximum current that can pass safely from the LED and give max. brightness. 

Consider the loop ABCDA,

(To know more about Kirchhoff Laws and how to use them from basics, refer to this article.) – Tackle Circuits using Kirchhoff’s laws

Applying KVL for the loop ABCDA,

$9 – IR – 2 = 0$

$IR = 7$

$0.02R = 7$

$R = 350\,\Omega$

Now, taking a resistor with greater resistance is completely fine. The only consequence of it will be the decrease in current passing through the LED, which will make the LED glow dimmer

Note:

The voltage drop across different colour LEDs is different. This is because they emit different colours as well. The following table gives the data about the voltage drops across different colour LEDs :

So, this is how we limit the current using the resistor, hence protecting our sensitive components from getting damaged.

2.2 Controlling the Voltage:

Another very important use of Resistors is to control the voltage at a region/point in the circuit. 

Let’s take an example.

Suppose that you have a mini-circuit designed that needs a 5V supply to work/operate. And again, you are having my 9V battery itself. So it’s obvious that you can’t directly give the 9V supply to the mini-circuit. It would blow up!! 

Solution: To tackle this problem, we can design a voltage-divider circuit. 

Consider the loop ABCDA.

• In the circuit below, our main aim is to get 5V at ‘H.’ 
• So, we need a resistor that can make a voltage drop of 4V. But this alone resistor won’t serve the purpose, as for a complete loop, the sum of potential differences should be zero. (KVL)
• Basically, we need one more resistor that can do the voltage drop of  the remaining 5V

Analysis of Circuit :

Let the current in the circuit be ‘i’

$\text{Potential difference across } R1 = i(R1) = 4V$ –(1)

$\text{Potential difference across } R2 = i(R2) = 5V$ –(2)

From (1) and (2),

$\frac{R1}{R2} = \frac{4}{5}$

I have R1 as 12 $k\Omega$. I substitute it in the above ratio to get my R2

$R2 = \frac{5 \times 12}{4} = 15k\Omega$

Also, we can get the current value if we want:

Applying KVL for the loop ABCDA,

$9 – i(R1) – i(R2) = 0$

$9 – i(12 \times 10^{3}) – i(15 \times 10^{3}) = 0$

$i = 3.3 \times 10^{-4}\,A$

With this circuit, we have created an outlet pin from where 5V can be used as the power source for the mini-circuit !!

In this Article, we are going to discuss one of the very important and most discussed methods in the chapter on electric circuits, that is Kirchhoff’s Laws. It’s used mainly in order to analyze circuits.

By analyzing a circuit, we mean :

• Finding the current flowing in a branch of the circuit
• Finding the potential of a point in a circuit
• Finding potential difference across the electrical components (resistors, capacitors, inductors, etc.)

There are a lot of other techniques as well to simplify and solve the circuits. But when everything fails, this works!

---

1. What are Kirchhoff’s Laws?

Kirchhoff’s Current Law (KCL) :

Statement: “The sum of all the currents entering a junction is equal to the sum of all the currents leaving the junction.”

Explanation :

Kirchhoff’s Voltage Law (KVL) : 

Statement: The sum of the potential differences across all the circuit elements for a closed loop is always zero

---

2. How to Apply Kirchhoff’s Laws in Circuits?

Now, comes the part of where to give plus(+) and where to give minus(-)

For this, just go by the definitions, and anything that opposes the definition gets the opposite sign.

Resistor: It’s a device that causes a potential drop, and the drop happens in the direction of current. So if we move in the direction of the current (through the resistor), the voltage has to drop !!

Va is potential at A, while Vb is potential at B

In this case above, the equation can be written as    Va – iR = Vb

Battery: Just look at ‘our direction’. If we are moving from the positive terminal of the battery to neagtive terminal of the battery, the voltage is going to decrease (Obvious)

In the above case, the equation can be written as $Va – E = Vb$

We focus on circuits containing batteries and resistors in this article. Getting a grip on this type of circuit would bring us to a position to easily deal with circuits containing capacitors and inductors as well

---

3. Easy to Moderate Level Examples :

Q.1 Find the current flowing in the loop, and also plot a graph that keeps track of the potential across the circuit

Solution :

• We first decide the current direction in the loop ABCDA 
• Then, we decide the direction in which we are going to move and, according to start moving from that point (here A) around the circuit. (Here, we move in A-> B -> C -> D -> A)
• Apply Kirchhoff’s law as discussed. (This example will make it a lot clearer)

Starting from A ->B,

We encounter a 12V battery. As discussed, only consider ‘our direction’. Here, we move from the negative terminal to the positive terminal, hence we have a potential rise. Hence, 

$+12$

For 2ohm resistor, we are moving in the direction of the current, so the potential should drop. Hence, the equation till now will become 

$+12-2i$

For 4ohm resistor, again we are moving in the direction of current, so again the potential should drop. Equation is :

$+12 – 2i – 4i$

For a 9V battery, we are moving from the positive terminal to the negative terminal, so potential drops over here. Hence,

$+12 – 2i – 4i – 9$

We have completed writing the sum of potential differences across all the elements in the circuit (all were present in A -> B). And, according to Kirchhoff’s Voltage Law, this sum should be zero. Therefore,

$+12 – 2i – 4i – 9=0$

$i=0.5 A$

The answer is positive, which implies that the assumed direction of current is correct.

We draw the graph to keep track of the voltage rise and drops across the elements (components)

On the Y-axis, we have the Voltage (in volts), and we keep a track of potential wrt the components.

– In this, we consider the negative terminal of a 12V battery to be at 0V (i.e., our reference).

It’s mandatory to have a point with 0V in any electric circuit. This is because potential at a point can be defined only when the reference has been set.

Note: There is no potential drop or rise in the wire (it’s constant). Wire can be described as a medium to carry forward the potential without making any changes to it. 

---

Question-2: Find the currents in the different resistors shown in the figure below.

Solution :

We give markings first so that it’s easier for us. For each loop, we consider a new current. Let’s do this much first.

• i₁ for loop ABGHA
• i₂ for loop BCFGB
• i₃ for loop CDEFC

Now, if we see carefully, in the path G-> H -> A -> B, only current i1 will be flowing. But for the branch BG, we have i1 as well as i2 coming into the picture since it’s a common branch to loop ABGHA and loop BCFGB.

Hence, considering i₁ > i₂ and also i₂ > i₃ (you may consider it either way),  the current distribution in all the branches becomes,

(Observe that KCL is also being followed)

Let’s go loop by loop. First, we take loop ABGHA (it means we start from A and end at A)

Equation is: 

$-2i_{1}-4(i_{1}-i_{2})-2+2-2i_{1}=0$

$-8i_{1}+4i_{2}=0$

$i_{2}=2i_{1}$ –(1)

Coming to loop GBCFG (starting from G)

p

Moving to loop CDEFC (starting from C)

Substitute (1) and (3) in equation (2) for getting value of i2,

We get,                                                                                                  

So, we can conclude that there is no current flowing through any of the resistors.

---

Conclusion:

Hence, with this, we have learnt how to apply Kirchhoff’s Laws and also discussed some problems based on this. But Kirchhoff’s Laws can also be used to calculate equivalent resistances of different networks. As I have already said, when everything fails, this would definitely work because KCL and KVL are based on fundamentals, and fundamentals never fail.