Circuit Analysis using Kirchhoff’s Laws | Solved Examples – Part 2

In this article, we will be discussing some interesting problems and applications of Kirchhoff’s Laws. The questions are lengthy, but at the same time, they are perfect for doing revision. A very important application of Kirchhoff’s Laws is its use to find the equivalent resistance for a given network

1. Interesting Question:

Question-1:

In the circuit shown in the figure below, E, F, G, and H are cells of emf 2 V, 1 V, 3 V, and 1 V, respectively. The resistances 2 Ω, 1 Ω, 3 Ω, and 1 Ω are their respective internal resistances. Calculate
(a) the potential difference between B and D, and
(b) the potential differences across the terminals of each of the cells G and H.

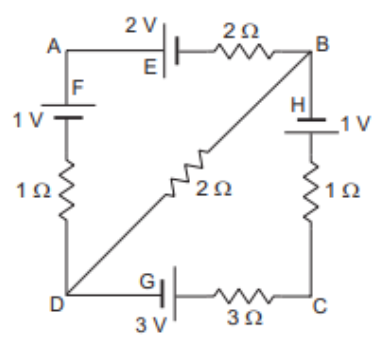
Solution: 

We can clearly see two loops over here. And we consider 2 currents, i₁ and i₂, in each of the loops. It’s completely our choice, whether to consider the current in a clockwise or in an anticlockwise direction. Here, we consider i₁ to be clockwise in loop ABDA, while i₂ is anticlockwise in loop CDBC.

Refer diagram below.

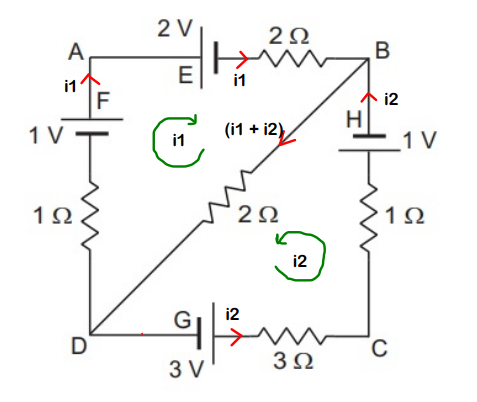
Again same procedure as we have discussed in Part-1, 

Consider one loop at a time. First, let’s apply KVL for loop ABDA:

$-2 – 2i_1 – 2(i_1 + i_2) – i_1 + 1 = 0$

$5i_1 + 2i_2 = -1 \quad \text{—(1)}$

Coming on to the next loop, CDBC, 

$3i_2 – 3 + 2(i_1 + i_2) + 1 + i_2 = 0$

$3i_1 + i_2 = 1 \quad \text{—(2)}$

On solving equations (1) and (2),

$i_2 = \frac{6}{13}$ and $i_1 = -\frac{5}{13}$

Here, i₂ is positive while i₁ is negative, which implies that the sense of i₂ is the same as considered (anticlockwise) while for i₁, it’s opposite to what we considered (i.e., in reality, it’s moving in an anticlockwise sense)

Actual situation :

For marking the potentials, we need a reference. We choose the negative terminal of 3V (at G) to be at 0V

Part-(a)

We need to basically find $V_B – V_D$

We apply KVL while going from B to D,

$V_B – 2\left(\frac{1}{13}\right) = V_D$

$V_B – V_D = \frac{2}{13}\, V$

Part-(b)

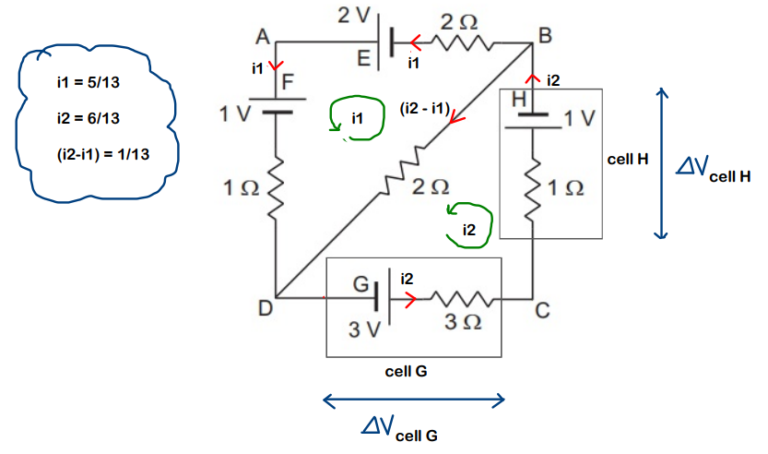
So, finding the potential difference across cell G is the same as finding the potential difference between points C and D, while finding the potential difference across cell H is the same as finding the potential difference between points C and B.

For cell G,

We need to find $V_C-V_D$

We apply KVL while going from C to D,

$V_C + 3i_2 – 3 = V_D$

$V_C + 3\left(\frac{6}{13}\right) – 3 = V_D$

$V_C – V_D = \frac{21}{13}\, V$

For cell H,

We need to basically find $V_C-V_B$,

We apply KVL while going from C to B,

$V_C – (1)i_2 – 1 = V_B$

$V_C – 1\left(\frac{6}{13}\right) – 1 = V_B$

$V_C – V_B = \frac{19}{13}\, V$

2. Kirchhoff’s Laws to find Equivalent Resistance:

To find equivalent resistance across 2 points given :

• Assume a battery between the 2 points (having a voltage of your choice)
• Find the current passing through the battery
• From the relation R = V/I, the value of R is nothing but the equivalent resistance

Example: Find the equivalent resistance between the points a and b of the network shown in the figure below.

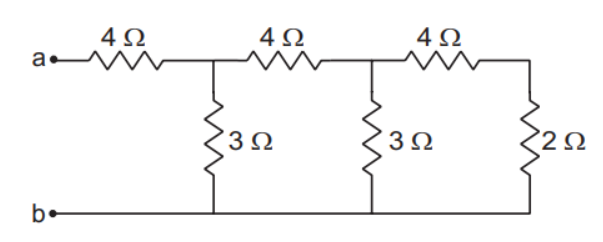
We have 2 points, ‘a’ and ‘b,’ and we need to find the equivalent resistance between these points

Step 1 – We consider a battery of 10V between ‘a’ and ‘b’

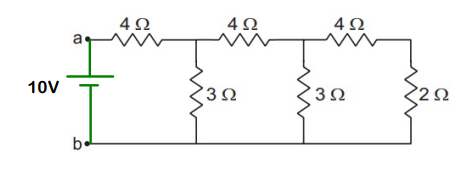
Step 2 – We need to find the current flowing through the battery (Here, it’s i1)

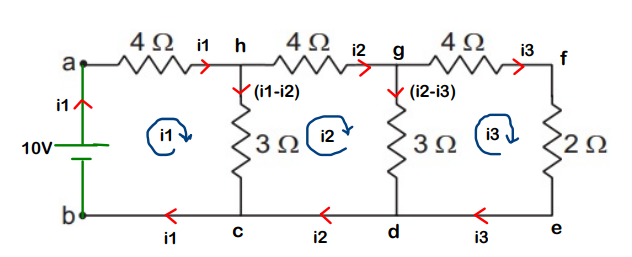
For loop ahcba,

$-4i_1 – 3(i_1 – i_2) + 10 = 0$

$7i_1 – 3i_2 = 10 \quad \text{—(1)}$

For loop hgdch, 

$-4i_2 – 3(i_2 – i_3) + 3(i_1 – i_2) = 0$

$-10i_2 + 3i_3 + 3i_1 = 0 \quad \text{—(2)}$

For loop gfedg,

$-4i_3 – 2i_3 + 3(i_2 – i_3) = 0$

$i_2 = 3i_3 \quad \text{—(3)}$

Substitute the i₃ value from (3) in (2). Solve the new equation with (1) to get the value of i₁

We get,

$i_1 = \frac{5}{3}\,A$

Step 3: Use the relation R = V/I. The value of R is nothing but the equivalent resistance between points ‘a’ and ‘b.’

$R = \frac{V}{I} = \frac{10}{\left( \frac{5}{3} \right)} = 6\,\Omega$

Therefore, the equivalent resistance between ‘a’ and ‘b’ is 6 $\Omega$

Conclusion:

Kirchhoff’s laws can be used in general to analyze all electric circuits. Though we have even faster techniques to solve the circuits, in case we are not able to use any of those, Kirchhoff’s laws will always be there for us !! 

This is what makes it important. 

Also, apart from its importance in just solving problems, it also gives us a very nice understanding of circuit analysis !!

All the Best

Keep Learning !!