What is the Perpendicular Axis Theorem, and where do we even use it?
In the last article, we learned about a very useful theorem called the ‘Parallel Axis Theorem‘. But as well know, it can be applied only when the 2 axes under consideration are parallel to each other.
But what if we want to know MOI about an axis that is not in the plane? Perpendicular Axis Theorem comes to our rescue
1. Perpendicular Axis Theorem

Conditions:
- Applicable to only planar 2-D bodies
- 3 axes to be considered
- 2 axes in the plane of the body, and 3rd should be perpendicular to both
- All 3 axes need to be concurrent (all of them should pass through the same point)
Descriptive Statement:
‘The moment of inertia of the planar body about an axis perpendicular to the plane is equal to the sum of moment of inertia of two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.’
(Observe that all the points have been covered in the ‘Conditions’ section above)
Mathematical Expression :
2. Examples based on Perpendicular Axis Theorem
Question: Find the moment of inertia Ip passing through the center of mass C of the square plate having mass M and side length L.
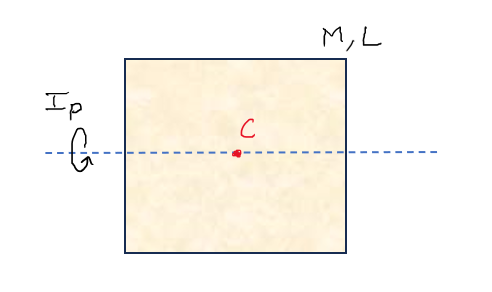
Solution:
Would there be any difference in the answer you get in Figure 1 and Figure 2 ? (Remember, it’s a square plate)
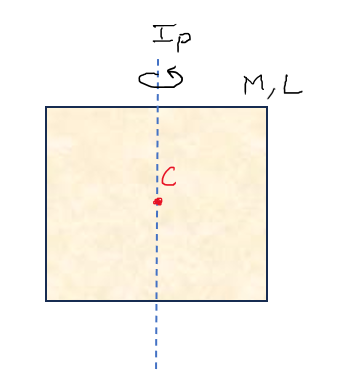

The answer is: NO! This is because of the beautiful symmetry that this square plate holds about the axis shown in both cases. There is the same mass distribution about the axis in both cases. That’s the reason you can’t really make out the difference!
Step-1:
Remember, we need 3 axes: 2 in plane and 1 perpendicular to them and concurrent. In this, we already got 2 planar axes (Combine figure 1 and figure 2). These will be our Ix and Iy. Hence, Ix = Iy = Ip. We get

Step-2:
Now, we also know the standard MOI for a square plate about an axis passing through C and perpendicular to the plane of the square plate. i.e. ML2/6. This is our Iz

Step-3:
Applying the perpendicular axis theorem,
3. Practice Question – Solve it yourself!
Now that we have learnt about the Parallel and Perpendicular Axis theorem, we are in a good state to apply this to a problem that requires both these theorems. (This itself is a good hint)
Question: Find the moment of inertia Ip for the uniform disc of mass M and radius R


