How to Use Kirchhoff's Laws to Solve Circuits? | KCL

In this Article, we are going to discuss one of the very important and most discussed methods in the chapter on electric circuits, that is Kirchhoff’s Laws. It’s used mainly in order to analyze circuits.

By analyzing a circuit, we mean :

Finding the current flowing in a branch of the circuit
Finding the potential of a point in a circuit
Finding potential difference across the electrical components (resistors, capacitors, inductors, etc.)

There are a lot of other techniques as well to simplify and solve the circuits. But when everything fails, this works!

Table Of Contents

1. What are Kirchhoff's Laws?
2. How to Apply Kirchhoff's Laws in Circuits?
3. Easy to Moderate Level Examples :
Conclusion:

1. What are Kirchhoff’s Laws?

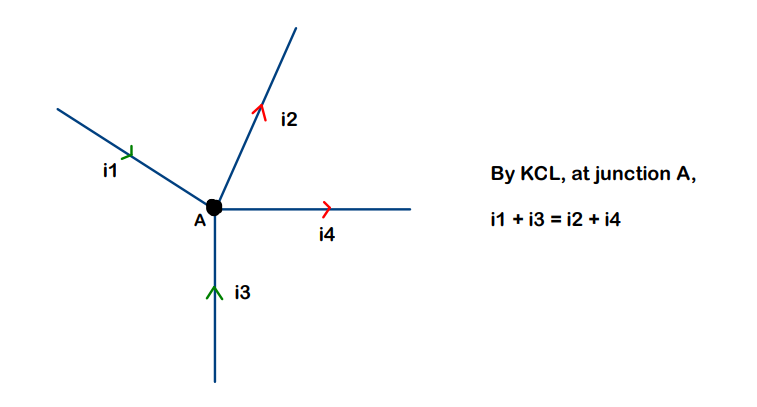
Kirchhoff’s Current Law (KCL) :

Statement: “The sum of all the currents entering a junction is equal to the sum of all the currents leaving the junction.”

Explanation :

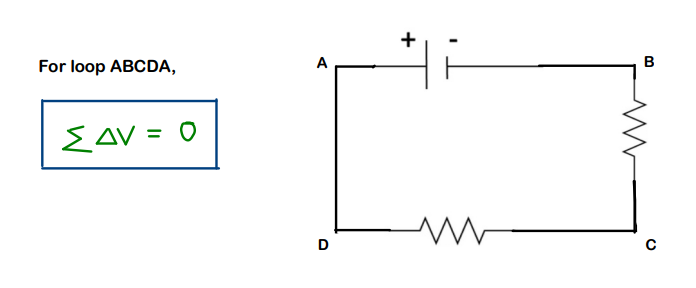
Kirchhoff’s Voltage Law (KVL) :

Statement: The sum of the potential differences across all the circuit elements for a closed loop is always zero

2. How to Apply Kirchhoff’s Laws in Circuits?

Now, comes the part of where to give plus(+) and where to give minus(-)

For this, just go by the definitions, and anything that opposes the definition gets the opposite sign.

Resistor: It’s a device that causes a potential drop, and the drop happens in the direction of current. So if we move in the direction of the current (through the resistor), the voltage has to drop !!

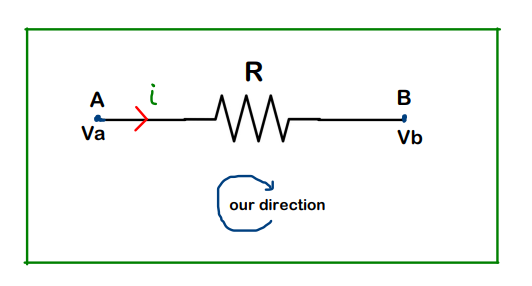
Va is potential at A, while Vb is potential at B

In this case above, the equation can be written as Va – iR = Vb

Battery: Just look at ‘our direction’. If we are moving from the positive terminal of the battery to neagtive terminal of the battery, the voltage is going to decrease (Obvious)

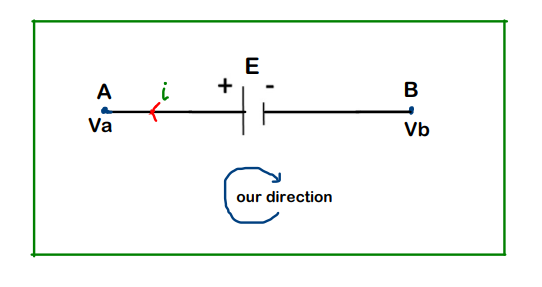
In the above case, the equation can be written as $Va – E = Vb$

We focus on circuits containing batteries and resistors in this article. Getting a grip on this type of circuit would bring us to a position to easily deal with circuits containing capacitors and inductors as well

3. Easy to Moderate Level Examples :

Q.1 Find the current flowing in the loop, and also plot a graph that keeps track of the potential across the circuit

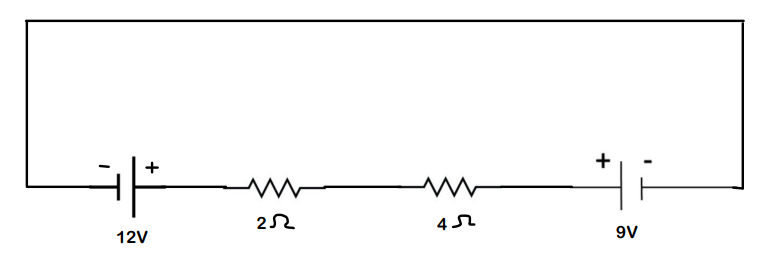
Solution :

We first decide the current direction in the loop ABCDA
Then, we decide the direction in which we are going to move and, according to start moving from that point (here A) around the circuit. (Here, we move in A-> B -> C -> D -> A)
Apply Kirchhoff’s law as discussed. (This example will make it a lot clearer)

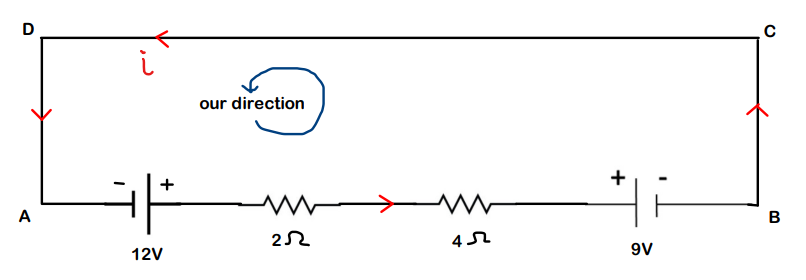
Starting from A ->B,

We encounter a 12V battery. As discussed, only consider ‘our direction’. Here, we move from the negative terminal to the positive terminal, hence we have a potential rise. Hence,

$+12$

For 2ohm resistor, we are moving in the direction of the current, so the potential should drop. Hence, the equation till now will become

$+12-2i$

For 4ohm resistor, again we are moving in the direction of current, so again the potential should drop. Equation is :

$+12 – 2i – 4i$

For a 9V battery, we are moving from the positive terminal to the negative terminal, so potential drops over here. Hence,

$+12 – 2i – 4i – 9$

We have completed writing the sum of potential differences across all the elements in the circuit (all were present in A -> B). And, according to Kirchhoff’s Voltage Law, this sum should be zero. Therefore,

$+12 – 2i – 4i – 9=0$

$i=0.5 A$

The answer is positive, which implies that the assumed direction of current is correct.

We draw the graph to keep track of the voltage rise and drops across the elements (components)

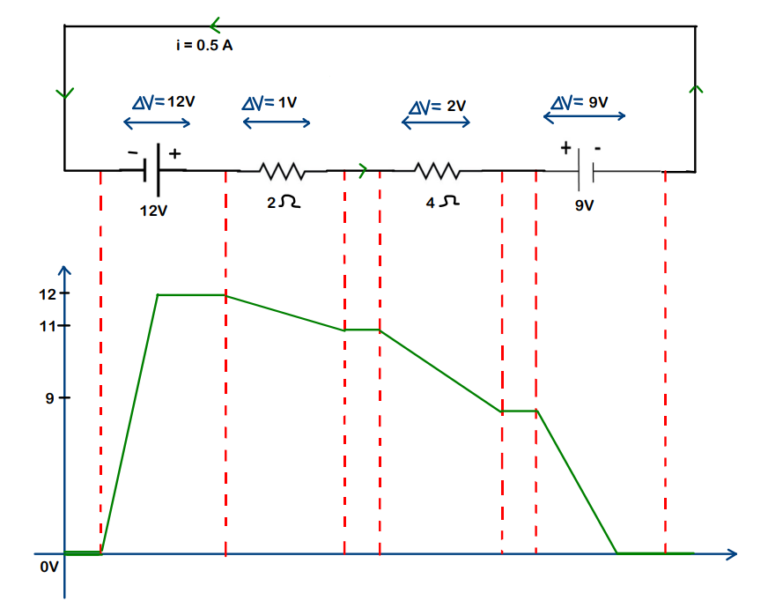
On the Y-axis, we have the Voltage (in volts), and we keep a track of potential wrt the components.

– In this, we consider the negative terminal of a 12V battery to be at 0V (i.e., our reference).

It’s mandatory to have a point with 0V in any electric circuit. This is because potential at a point can be defined only when the reference has been set.

Note: There is no potential drop or rise in the wire (it’s constant). Wire can be described as a medium to carry forward the potential without making any changes to it.

Question-2: Find the currents in the different resistors shown in the figure below.

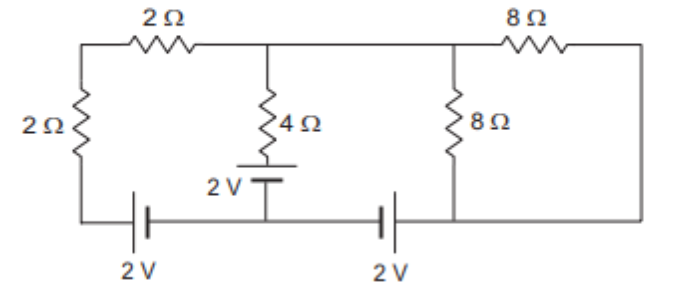
Solution :

We give markings first so that it’s easier for us. For each loop, we consider a new current. Let’s do this much first.

i₁ for loop ABGHA
i₂ for loop BCFGB
i₃ for loop CDEFC

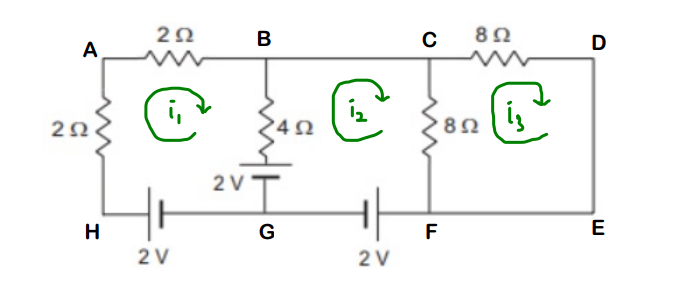
Now, if we see carefully, in the path G-> H -> A -> B, only current i1 will be flowing. But for the branch BG, we have i1 as well as i2 coming into the picture since it’s a common branch to loop ABGHA and loop BCFGB.

Hence, considering i₁> i₂ and also i₂ > i₃ (you may consider it either way), the current distribution in all the branches becomes,

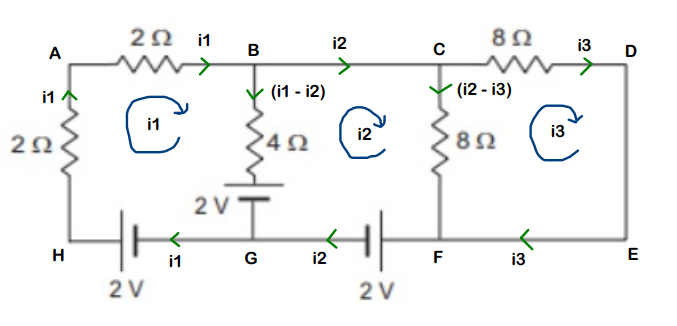
(Observe that KCL is also being followed)

Let’s go loop by loop. First, we take loop ABGHA (it means we start from A and end at A)

Equation is:

$-2i_{1}-4(i_{1}-i_{2})-2+2-2i_{1}=0$

$-8i_{1}+4i_{2}=0$

$i_{2}=2i_{1}$ –(1)

Coming to loop GBCFG (starting from G)

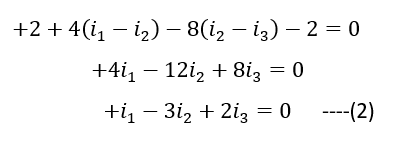
Moving to loop CDEFC (starting from C)

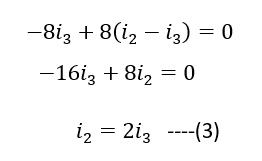
Substitute (1) and (3) in equation (2) for getting value of i2,

We get,

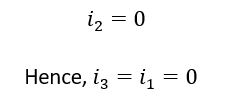
So, we can conclude that there is no current flowing through any of the resistors.

Conclusion:

Hence, with this, we have learnt how to apply Kirchhoff’s Laws and also discussed some problems based on this. But Kirchhoff’s Laws can also be used to calculate equivalent resistances of different networks. As I have already said, when everything fails, this would definitely work because KCL and KVL are based on fundamentals, and fundamentals never fail.

How to Use Kirchhoff’s Laws to Analyze Circuits?