How to Solve Pulley Block Problems? | Trick Explained

by

Pulley Block Problems are very common in high school physics and mainly come under Newton’s Laws of Motion (NLM) chapter. These concepts are frequently asked in exams such as JEE Mains and even JEE Advanced. 

Time becomes an important factor in such competitive examinations, especially JEE Mains. So, it’s always better to have some short tricks to be faster and save time. But, still, I would like to emphasize the fact that concept>>tricks

Table Of Contents
  1. Rules to apply the Trick:
  2. Easy Examples based on Pulley Problems
  3. Moderate to Difficult Examples on Pulley Problems
  4. Conclusion :

Rules to apply the Trick:

Remember the rules :

  • Only one string at a time
  • On the string –> ‘minus’ sign (Recall the -ve charge sign on ions from chemical bonding because that’s how I kept it in my mind)
  • Away from the string –> ‘plus’ sign

How to use this trick in solving pulley block problems?

Steps:

  1. Mark the points on the string such that whole string is covered (starting to end)
  2. For pulleys, mark for the points- where the string first comes in contact with the pulley (point 2) and where the string leaves the contact with the pulley (point 3)
  3. Now start from one end ( say point 1). The relation will be as follows (-Va + 0 + 0 +Vb) 

Why?

-Va because Va is going on the string

+0 because point 2 is connected to the pulley and the pulley is at rest

+0 point 3 is connected to pulley and pulley is at rest

+Vb because point 4 is connected to block B, and Vb is going away from the string

Finally equate everything to zero i.e. (-Va + 0 + 0 +Vb = 0)

Final Answer: We get Va = Vb

Easy Examples based on Pulley Problems

Q.1 Write down the constraint relation between velocities of block A and block B by referring the image of setup given below

Solution :

Constraint relation can be written as : (Applying trick, starting from block A)

−vA+0+0+vB+vB+0+0+0=0– v_A + 0 + 0 + v_B + v_B + 0 + 0 + 0 = 0

Shown below is the breakdown of what each term in the above expression represents:

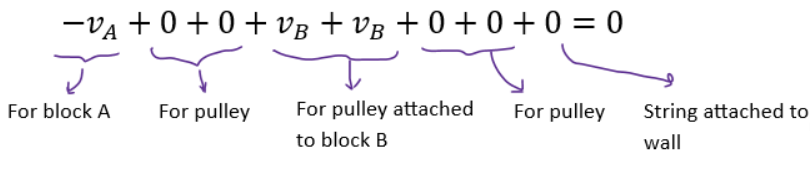
On simplifying, we get:

vA=2vBv_A = 2v_B

Q.2 Write down the constraint relation between velocities of block A and block B by referring the image of setup alongside.

Solution:

We start from block A (Just move along the string one-by-one) :

−vA+0+0+vB+vB+0=0– v_A + 0 + 0 + v_B + v_B + 0 = 0

vA=2vBv_A = 2v_B


Q.3 Write down the constraint relation between velocities of block A and block B by referring the image of setup alongside.

Solution : Let’s start from block A

We start from block A (Just move along the string one-by-one) :

−vA+0+0+vB+vB+0=0– v_A + 0 + 0 + v_B + v_B + 0 = 0

vA=2vBv_A = 2v_B


Moderate to Difficult Examples on Pulley Problems

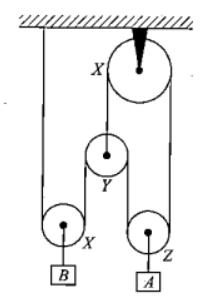
Question 4:

The figure alongside shows a system of four pulleys with two masses, A and B. Find, at an instant:

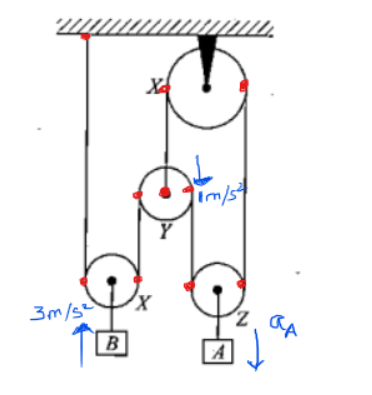
(a) Speed of block A when the block B is going up at 1 m/s and pulley Y is going up at 2 m/s.

(b) Acceleration of block A if block B is going up at 3 m/s² and pulley Y is going down at 1 m/s².

Solution:

Part (a) :

 (Lets start from the point near the rigid support)

The constraint relation can be written as:

0−1−1+2+2+vA+vA+0+0−2=00 – 1 – 1 + 2 + 2 + v_A + v_A + 0 + 0 – 2 = 0

2vA=02v_A = 0

∴vA=0\therefore \; v_A = 0

Part (b) :  Again we start from the point attached to the rigid end 

(Note that the derivative of velocity wrt time is acceleration. So once you get the velocity constraint relation, just taking its derivative wrt time will give you the constraint relation for accelerations)

The constraint relation can be written as:

0−3−3−1−1+aA+aA+0+0+1=00 – 3 – 3 – 1 – 1 + a_A + a_A + 0 + 0 + 1 = 0

2aA=72a_A = 7

∴aA=3.5m/s2\therefore \; a_A = 3.5 \,\text{m/s}^2

Question 5:

Write the constraint relations between block A and block B in the setup shown in the image alongside 

Solution:

Recall that this trick can only be applied to one string at a time!

So, we take velocity of pulley X as Vx as shown in figure below and we start applying trick from block A end

The constraint relation can be written as:

vA+0+0+0+0+0+0+0+vX+vX=0v_A + 0 + 0 + 0 + 0 + 0 + 0 + 0 + v_X + v_X = 0

2vX=−vA2v_X = -v_A

But, we need relations between Vb and Va

The constraint relation can be written as: (Starting from block B)

−vB+0+0−vX=0-v_B + 0 + 0 – v_X = 0

vX=−vBv_X = -v_B

On Substituting vX value to get the relation between the velocity of A and the velocity of B,

We get,

vA=2vBv_A = 2v_B

Question 6:

Find the speed of block B when the wedges A and C are moving toward each other with speed v and the strings connected to block make an angle θ with the vertical, as shown in the figure alongside

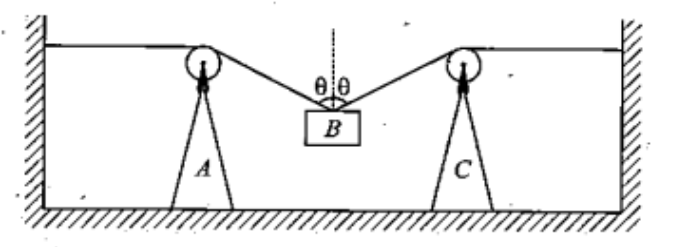
Solution: 

As we discussed, only the velocity component along the string are to be considered

Starting from the green colored star (*) mark

Same approach, mark all the points  on the string first

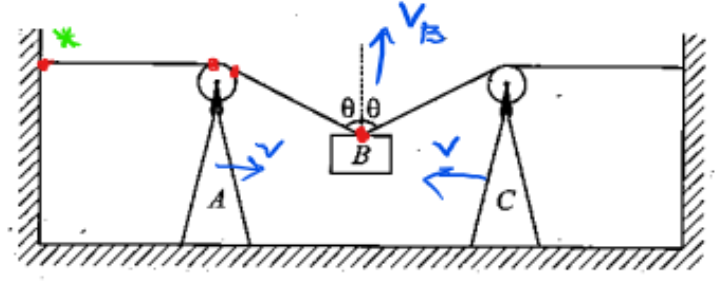
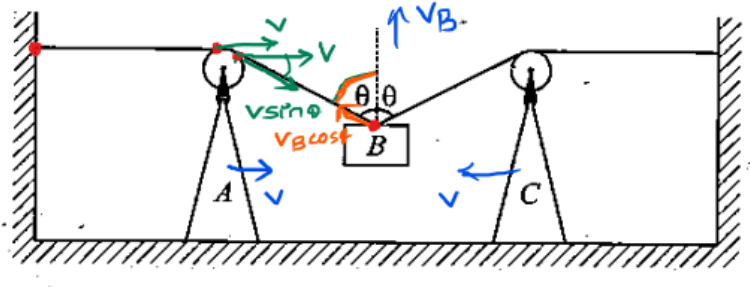
The constraint relation can be written as: (Starting from block B)

0+v−vsin⁡θ−vBcos⁡θ=00 + v – v\sin\theta – v_B \cos\theta = 0

vB=v(1−sin⁡θ)cos⁡θv_B = \frac{v(1 – \sin\theta)}{\cos\theta}

But, we know that the value of VB (RHS) from the above expression is always going to be positive since,

−1≤sin⁡θ≤1-1 \le \sin\theta \le 1

So, the assumed direction of VB (upwards) is also correct!

Conclusion :

So, over here, we end this article. Do practice some more string pulley constraint problems using this trick. But also don’t miss out on the actual procedure. Tricks should always be your secondary option !!

 We will keep coming up with more such articles to help you in your preparation !! Thank you for your time.

Have a good day!

Leave a comment