In the last article, we got to know a very useful theorem called ‘Parallel Axis Theorem’. But as well know, it can be applied only when the 2 axes under consideration are parallel to each other.
But what if we want to know MOI about an axis which is not the plane ? Perpendicular Axis Theorem comes to our rescue*
Topics Covered :
- Perpendicular Axis Theorem
- Example
- Miscellaneous Activity (Parallel + Perpendicular)
1. Perpendicular Axis Theorem

Conditions :
- Applicable to only planar 2-D bodies
- 3 axes to be considered
- 2 axes in plane of the body and 3rd should be perpendicular to both
- All 3 axes needs to be concurrent
Descriptive Statement :
‘The moment pf inertia of the planar body about an axis perpendicular to the plane is equal to the sum of moment of inertias of two perpendicular axis concurrent with perpendicular axis and lying in the plane of the body’
(Observe that all the points have been covered in ‘Conditions’ section above)
Mathematical Expression :

2. Example
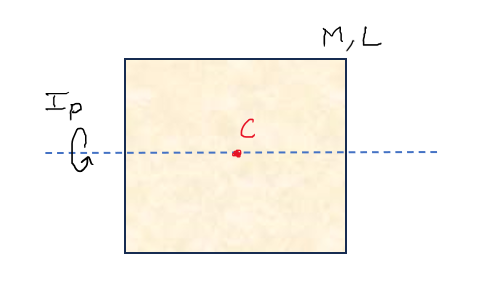
Question : Find the moment of inertia Ip passing through center of mass C of the square plate having mass M and side length L.
Solution :
Would there be any difference in the answer you get in Figure 1 and Figure 2 ? (Remember, it’s a square plate)
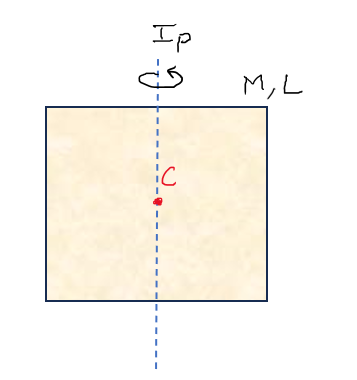

The answer is : NO ! This is because of the beautiful symmetry that this square plate holds about axis shown in both the cases. There is the same mass distribution about the axis in both the case. That’s the reason, you can’t really make out the difference !
Step-1 : Remember, we need 3 axes : 2 in plane and 1 perpendicular to them and concurrent. In this we already got 2 planar axis (Combine figure 1 and figure 2). These will be our Ix and Iy. Hence, Ix = Iy = Ip. We get

Step-2 : Now, we also know the standard MOI for square plate about an axis passing through C and perpendicular to plane of square plate. i.e. ML^2/6. This is our Iz

Step-3 : Applying perpendicular axis theorem

Solve it yourself !
Now that we have learnt about Parallel and Perpendicular Axis theorem, we are in a good state to apply this to a problem which requires both these theorems. (This itself is a good hint)
Question : Find the moment of inertia Ip for the uniform disc of mass M and radius R



